Part A: Concise and effective ways of presenting a Jigsaw design
A1: What is different about Jigsaw?
To repeat: So what distinguishes the Jigsaw learning design?
A1. The teacher is not the subject matter expert.
This aspect has a long history (traditional seminars are supposed to be like this, but seldom are in practice), but also has promising modern reincarnations such as having students write test items for each other. This is sometimes called student generated content (SGC), and/or Contributing-student pedagogy (CSP).
A2. The mutual dependence of the students: the majority of one's learning depends on what other students teach.
B. The cross-cutting groups: each learner is a member of two different groups with (usually) no other members in common.
The groups
(This is to explain the nature of the groups, how they differ, and the terminology that will be used to distinguish them.)One kind (the "self-teach", expert groups) are co-experts helping each other prepare material for teaching other students; the other kind (the "cross-teach", home groups) are where students teach each other different parts ("topics") of the overall subject. However in many near-Jigsaw designs, the cross-teach groups are either the whole class, or individuals with different learning goals from each other (example1: as in a traditional seminar, each student constructs something different for the class; example2: each reflecting on their own different, personal professional practice; although helped overall by comments from a group).
(N.B. the terms "collaborative" vs. "cooperative" are not helpful in articulating the contrast between the two group types here. The self-teach groups have the same product goal as each other, and bring their planned presentations up to the best standard that the union of their similar expertise can manage. The cross-teach groups are exchanging an essential service which their fellows cannot provide; a reciprocal service delivery, divided by specialism.)
| Group names | ||
|---|---|---|
| Type 1 | Type 2 | |
| Self-teach (one topic) | Cross-teach (all topics) | Preferred here |
| Expert | Jigsaw | Aronson's terms |
| Research | Learning | Ann Brown's terms |
| Reading | Discussion | Benton's terms |
| Preparation | Exchange | |
| Author | Reviewing? Learning? | |
| Consulting | Home | |
| Union of peer knowledge | Reciprocal service delivery, divided by specialism | |
| Union, pooling | Reciprocal | SLH's |
| Joint product | Joint means (to different ends) | |
Aronson's summary of the procedure
Aronson's way (slightly adapted) of summarising the design is:- Students are divided into a 5 or 6 person jigsaw group. The group should be diverse (e.g. in terms of prior knowledge and/or level of effort).
- The content is divided into 5-6 segments (one for each member)
- Each student is assigned one segment to learn. Each student should only have direct access to their own segment.
- Students should be given time to read over their segment at least twice to become familiar with it. Students do not need to memorize it.
- Temporary experts' groups should be formed in which one student from each jigsaw group joins other students assigned to the same segment. Students in this expert group should be given time to discuss the main points of their segment and rehearse the presentation they are going to make to their jigsaw group.
- Students come back to their jigsaw group.
- Students present their segment to the group. Other members are encouraged to ask questions for clarification. This is small group, dialogic teaching.
- A test on the material should be given at the end so students realize that the sessions are not just for fun and games, but that they really count.
A2: More visual representations
A number of different representations, besides prose, are useful for presenting Jigsaw designs to colleagues or to students in a class with clarity, detail, and brevity. These are:- Prose e.g. Part A1 above.
- Bullet lists: a mixture of language (often not strictly grammatical) and visual structure.
- Diagrams
- Tables
- Slides
Here are some examples, which are used to express what makes one Jigsaw design for a particular class different from another (given the understanding of essentials expressed in the previous section).
Representation 1: List of bullet points
Use numbers; get across there are 2 group types; tell the size of the class, the size of each type of group, and the number of people in each type of group; and the cycle time (once per week or once per course?).
Aronson's version of Jigsaw for a school class:
- Education Level: US school
- Each learner is a member of not 1 but 2 groups.
- Total number of learners (class size) ≈ 20-30
- Distinct topics learned: ≈ 4
- Cross-teach groups: Group size ≈ 4 (number of groups ≈ 7)
- Self-teach groups: Group size ≈ 7 (number of groups ≈ 4)
- Cross-teach groups: Group size ≈ 4 (number of groups ≈ 15)
- Motivation for learning from peers: regular class assessments, and no other source of knowledge.
- No information / communication technology, nor virtual learning environment used.
- Cycle time: Done every 1-2 class meetings; repeated throughout the term (i.e. about ≈ 10 times). (So not one piece of "groupwork" per semester.)
A case from a CPD workshop:
- Education Level: Professional / CPD.
- Each learner is a member of not 1 but 2 groups.
- Total number of learners (audience size) ≈ 60
- Distinct topics learned: ≈ 4
- Self-teach groups: Group size ≈ 15 but subdivided ad hoc into discussion groups of 3-6 (number of topic groupings 4, but subdivided ad hoc into ≈ 12 discussion groups)
- Cross-teach groups: Group size ≈ 4 (number of groups ≈ 15)
- Motivation for learning from peers: small, it is just a demo.
- No information / communication technology, nor virtual learning environment used.
- Cycle time: done once (within a 2 hour workshop).
Ann Brown:
- Education Level: US middle school grade 6 (11-12 year olds?)
- Class size: ≈30.
- Each learner is a member of not 1 but 2 groups.
- Distinct topics to learn: 5
- Self-teach (expert) groups: 5 groups of size 6
- Cross-teach (jigsaw) groups: 6 groups of size 5
- Motivation for learning from peers: The cross-teach groups give a presentation to outsiders on the whole subject (all topics).
- In this case every learner prepares 1 topic, hears all 4 of the other topics, and gets to teach 4 other students about their own topic.
- Computer technology used for pupils to prepare materials for others.
- Cycle time: The whole design takes 8-10 weeks; and is (ideally) repeated 3 times per year.
- There are other features of her design beyond the basic Jigsaw idea focussed on here (Brown & Campione, 1996).
Honeychurch's first year philosophy tutorials:
- Education Level: University year 1.
- Class size = 14.
- Distinct topics learned: 3
- Self-teach (expert) groups: 3 groups of size 4-5
- Cross-teach (jigsaw) groups: 1 group of size 14 i.e. plenary.
- Motivation for learning from peers: capturing understanding in notes, ready for exam revision.
- Cycle time: Done once per week, repeat throughout semester
- Rotate who within each self-teach groups does the exposition to the whole class.
- In this case every learner hears 3 topics and gets to inform 14 others of their own topic once or twice per semester.
My final year modules?:
xxBullet lists: reprise
Such bullet list summaries of a particular Jigsaw design can and should of course be customised for the exact case e.g. adding some relevant comment to make a point. However here are two broad types of use, at least on this web page: those above aimed at colleagues, which need to mention some things about the specific application; and those in the latter parts of part B3 which assume some generic context and are comparing alternative designs.
Representation 2: Diagram emphasising how individuals cross-connect groups
 (Click on the image to see the full size version.)
(Click on the image to see the full size version.)
But this seems to need to be drawn by hand: too much effort for regular use, but perhaps useful in giving talks.
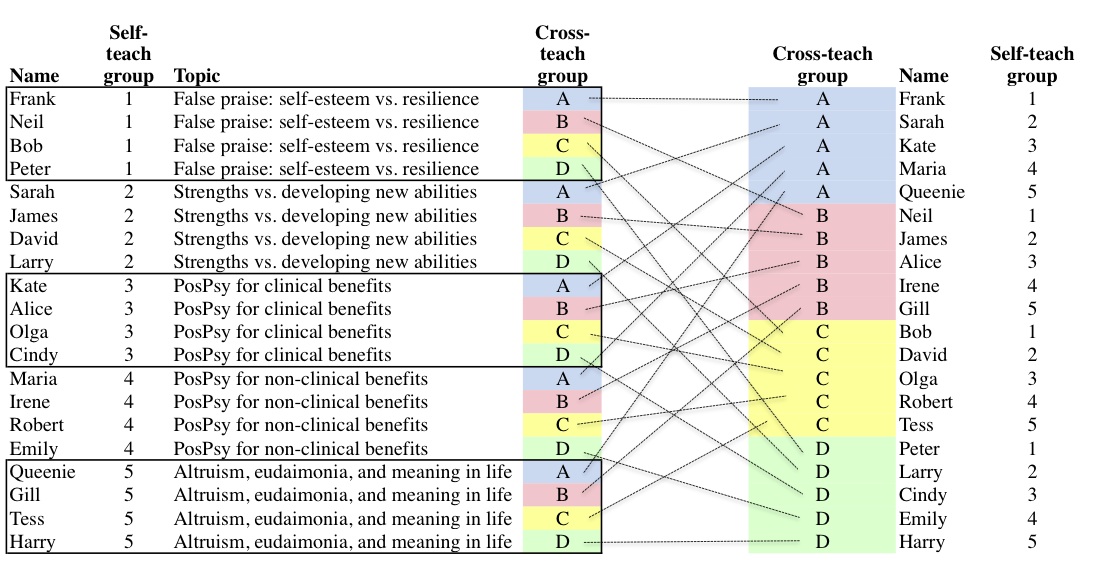
Representation 3: Student allocation tables (in a handout, probably generated in a spreadsheet)
If giving a handout to a class, you need to create and distribute a list of students, with TWO group names against each student from two different, cross-cutting, sets (because each will be in 2 groups not 1). A single table specifies all allocations (although in a big class, finding what you want in the table becomes harder).In this first example self-teach groups are emphasised and have their topics listed, while cross-teach groups of 5-6 members (denoted by letters) have to organise meetings which are not specified there. In the second example this is reversed.
| A few lines sampled from a table emphasising cross-teach groups | The whole table | |||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
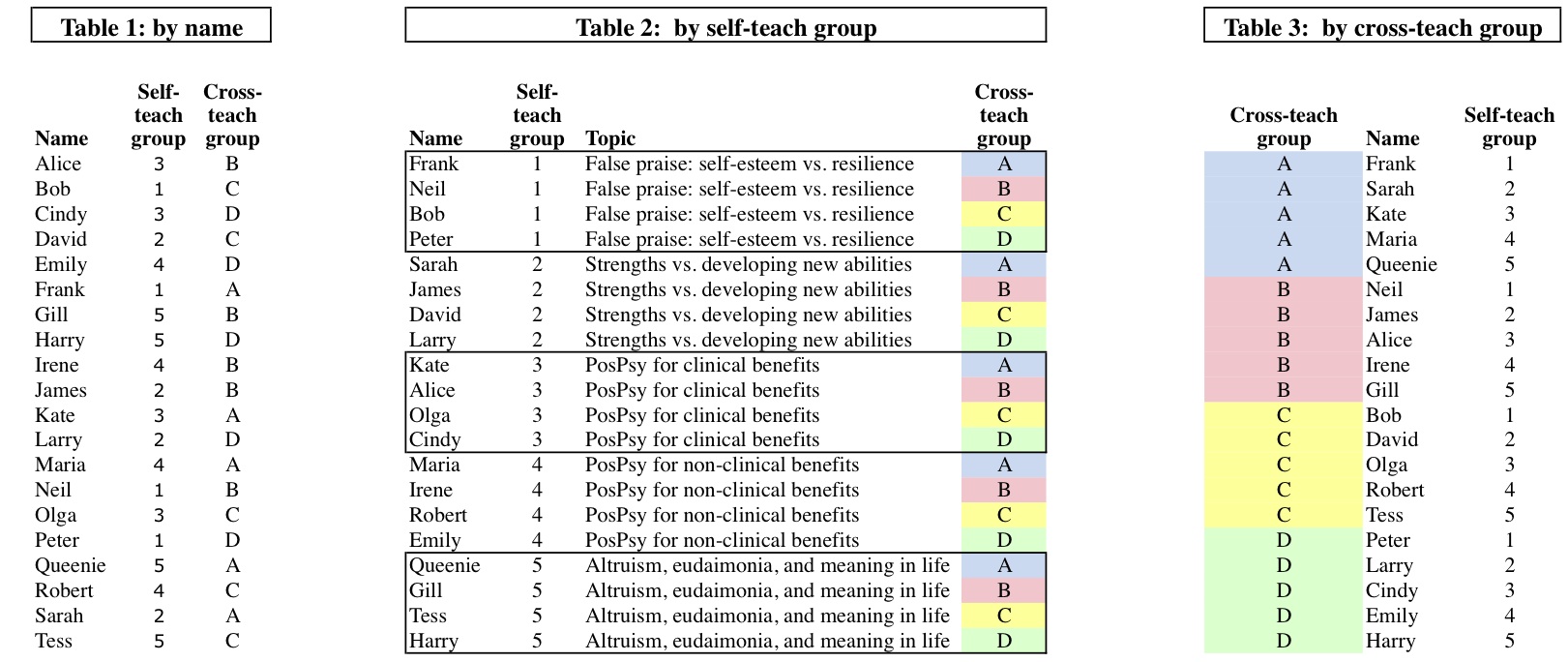
Representation 3B: Multiple allocation tables
In practice, the allocation of students to groups is better shown in three redundant tables sorted respectively by name (so that students can look up their own assignments), by group type 1, and by group type 2 so that they can see their fellow group members in each of their groups.Example 2
In this example:- Class size = 20.
- Distinct topics to learn: 5
- Self-teach (expert) groups: 5 groups of size 4.
- Cross-teach (jigsaw) groups: 4 groups of size 5.
- In this case every learner hears every topic and gets to inform 4 others of their own topic. And learners can be exactly evenly distributed so that groups of the same kind are of identical size.
Example 3
In this example:- Class size = 181.
- Distinct topics to learn: 31
- Self-teach (expert) groups: 31 groups of size 5-6.
- Cross-teach (jigsaw) groups: 31 groups of size 5-6.
- In this case every learner hears 4-5 topics and gets to inform 4-5 others of their own topic. An extra report-back session in self-teach groups could pool all 18 of the 31 topics in principle.
- In this case (with a class size that is a prime number) groups of the same kind must vary in size by at least 1 as the class size isn't exactly divisible.
- This design has abandoned direct teaching of every topic to every student: see part B below.
Representation 4: Slides for showing an audience where to go now
If getting the class to break into groups to talk to each other, then one kind of slide to display is here. They need to move physically, and they need to have a map visible as they move: so a projected slide is what is needed.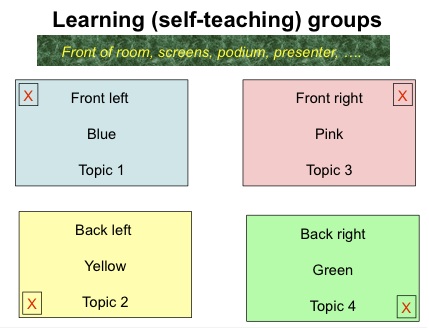

Put up SLH's slides here?
Part B: The underlying and emerging issues in scaling up
In this part, a sequence of issues is reviewed or introduced which affect how you compose a specific Jigsaw design, and which escalate somewhat as class size rises i.e. some issues only make a difference with larger class sizes. First (in section B1) I list the issues underlying the basic designs already introduced. Then, after collecting some basic numerical relationships between groups sizes in Jigsaw, I divide the further issues into phases and deal with each in turn.B1: The underlying issues in designing a Jigsaw activity
The main underlying issues for all designs including the small sizes typical of schools (20-30), were mostly mentioned in part A above, and are the following.Issue 1: SGC: student authoring
This aspect has a long history (traditional seminars are supposed to be like this, but seldom are in practice), but also has promising modern reincarnations such as have students write test items for each other. This is sometimes called Student Generated Content (SGC), and/or Contributing-student pedagogy (CSP).Having basic expository content provided not by the teacher but by students comes in many forms. The content need not necessarily be the main course content: it might be test items, introductions, etc. It has many potential advantages: gives students confidence, trains them in teaching themselves (the most valuable skill they can ever learn in an education system), they are inherently more in tune with their audience (other peers) in explaining things. It is an ancient tradition: that is what seminars are supposed to be.
Issue 2: Student reciprocal dependence
The next underlying element that Jigsaw has is usually missing from many seminars as actually done in universities: having the learners dependent on each other, with no alternative source of knowledge. I.e. arranging that learners must use what other students produce. (The classic problem with seminars is that though each student may produce a "paper" or talk when required, the only real audience is the teacher, and other students do not actually need to learn from it.)With reciprocal dependence, student presenters take it much more seriously, and student listeners make questions and comments because they really need to clear up partial understandings. Using others' products need not be by learning from expository material. It might be producing a critique and giving feedback. It might be using test items others have produced. It might be using summaries not directly to learn, but to make an informed choice of which topics to select to learn for the exam.
Issue 3: Social Psychology effect of group bonding FROM joint tasks
When people succeed at a task together, they beome bonded. This effect is well established in Social Psychology (Sherif). This is contrary to our intuition: we tend to feel that we succeed at a joint task because we were bonded to start with. But our intuition is wrong about the direction of the causation. However it means that students may resist or hate a Jigsaw design at first. Aronson invented Jigsaw as an application of this effect: not primarily to cause learning, but to cause social bonding.Issue 4: Not just exposition; not just 1-group work; but TWO groups
In the true Jigsaw design, the activity isn't an exposition by the teacher nor any other single person. And it isn't just ordinary groupwork where a class divides into one kind of smaller group (which is generally either producing something together or discussing something between people of equal knowledge). It is based on two groups: one where personal preparation and learning is checked and improved with others tackling the same topic; and one where experts use their knowledge to teach others.It is learning from personal interaction (e.g. 1:3 teaching ratio) with someone who knows what you need to learn. It is thus essentially dialogic (based on discussion, although not on discussion about opinions on topics no-one really understands). It may be the only way to supply personal dialogic teaching in a mass education system.
Issue 5: Cross-cutting
I use the term "cross-cutting" to draw attention to how, by having each learner be part of two different groups, the class potentially becomes more integrated; whereas having a single type of habitual group means that the class is divided. (Learners get to know about four other people, but may interact even less with any others.) It is thus possible to start thinking about social networks, and connections at one or two removes; and how things may spread throughout the larger group i.e. the class. With large classes, while this diffusion is unlikely to become complete, Jigsaw is likely to make a bigger difference. It is easy to attend lectures with 100 other students, and never learn more than two or three people's names. With Jigsaw, that is more likely to be eight to ten people, who will each mention others, rather than being members of only your group.Ideas of "social integration" (Tinto) suggest this is one factor tending to reduce dropout, and increase student resilience when their education gets tough. It is also essentially Aronson's own motive for developing Jigsaw: to combat race segregation within school classes after US school "desegregation" forced pupils to be in the same room. Ordinary groupwork tends to be segregation into friendship groups, and to do little for or even harm to the integration of the class as a whole.
This issue interacts with whether the Jigsaw process is repeated e.g. weekly in that class, and whether group membership is maintained or remixed each time. For getting growing familiarity and (usually) smooth group functioning, fixing groups is better; but for maximising networking, and integration across the class, remixing might be better.
B2: The numbers
- Except by luck, a class cannot be divided into groups of exactly equal sizes. If the class size is a prime number (e.g. 23, 67, or 181) then it can never be done; but often in any case there are other reasons for fixing group size than divisibility into the class size: see "Issue 6" below.
- The number of topics (sub-parts of the overall subject) to be learned in one Jigsaw activity equals the number of the self-teach groups equals the minimum size of the cross-teach groups. E.g. with class size = 28 and number of topics = 4 = the minimum size of the cross-teach groups = the number of different kinds of self-teach groups; while 7 = the maximum size of the self-teach groups = the number of cross-teach groups.
- The converse isn't true: if you wish, you can subdivide self-teach groups and have more but smaller ones. Often you may not even have to pre-organise this: they'll naturally separate into more useful small groupings.
- Indirect coverage: As the number of topics grows in a big class,
personal cross-teaching of all topics isn't possible. However by adding the
idea of learners reporting back to their expert groups, after cross-teaching
has happened, learners could pool an account of the topics they have heard
about; at least in terms of the best they heard. This second-degree
relationship allows the number of topics each learner potentially hears about
to be calculated, where type1 means self-teach and type2 means cross-teach, as:
- They all learn one topic for themselves: 1
- They are directly taught by others in their cross-teach group: Type2size - 1
- and at second hand can hear about: (Type1size - 1) * (Type2size - 1)
- This adds up (where Type1size is the size of the self-teach/authoring
groups) to:
(Type1size * Type2size) - Type1size + 1 - For example with group sizes of 5 or 6, indirect coverage will cover 20 or more topics, while only 14-17 topics would exist for a class of 83 and those sizes.
B3: The three phases
As class numbers rise, there are three phases of Jigsaw design issues. Each tends to bring up new problems and partial solutions.Phase 1: Simple
With class size numbers up to about 30, it is quite possible to have a simple design with only two types of group. For example:- Class size = 28.
- Distinct topics learned: 4
- Self-teach (expert) groups: 4 groups of size 7.
↔ 8 groups of size 3-4, 2 groups for each topic. - Cross-teach (jigsaw) groups: 7 groups of size 4.
Issue 6: Uneven group sizes
[A] Why you usually have uneven numbersGroups of the same type cannot be exactly the same size when the class size isn't exactly divisible by the group size (which is inevitable when the class size is a prime number, and is often the case because other factors than class size determine group sizes). For example:
- Class size = 27.
- Distinct topics learned: 4
- Self-teach (expert) groups: 4 groups of size 6 or 7.
↔ 8 groups of size 3-4, 2 groups for each topic. - Cross-teach (jigsaw) groups: 7 groups of size 3 or 4.
[B] Why not have an odds and ends group much different in size?
In dividing a class into uneven groups, you can either have some the preferred
size and the rest just one learner more (or less) than the preferred number;
or else you can have all groups except one the best size, plus a single group
with the remainder (often with several fewer, or more, than the rest). In the
rest of this page, I've assumed that staying within one of the preferred group
size is best. However this really depends on what the reasons behind the
chosen preferred group size is (see next "Issue7"). And there can sometimes
be a good reason for one group being different in size. For example, the
"odd" group might be given the task of creating and maintaining an index to
the others groups' work, or a glossary to complement it, or ...
[C] What to do if students join late or drop out?
Especially in large university classes, it is usual for real participation to
change after group allocations have been made, both through dropouts and late
arrivals. It is best to be ready for this. Obviously if you're lucky new
arrivals will happen just after a dropout has emerged, and can replace them.
With uneven group numbers, it is obvious you should add a student to one of
the groups with a smaller number. If you are unlucky, then new arrivals fill
up the slots and trigger the need for a new group, and the need to redeploy
some existing students into it. For example, if the number of topics is 4,
then cross-teach groups will have 4 ideally, and some will have 5 if numbers
are uneven. When all groups have 5 you must, and when 4 groups have 5 it is
desirable, that you create an extra group and move 4 students (the new one
plus 3 redeployed) into it.
Issue 7: Validation by staff members
Even though the founding idea of Jigsaw (Issue 1) is that students play the role of subject matter expert, you may see a need in students for validation by a member of staff. Aronson's response was to add the expert groups to help with quality control of what got taught by learners. It is true too that student self-help groups (Peer Assisted Learning groups) frequently function well like that elsewhere, as do the expert groups in Jigsaw. Still, students may feel the need for a bit more.Ann Brown talks about this in terms of multiple sources of expertise: peers, older students/mentors, teaching staff, visiting (or remote consultations with) experts. However another angle is to identify this need as "validation" rather than authoritative subject knowledge. Students want to be sure not just that they got some fact right, but that they are giving reasons of the right kind (arguing like a philosopher in a philosophy class, citing evidence of the kind that a psychologist accepts in a psychology class, like a mathematician in a maths class), presenting at the right level (not too formal or too informal), discussing in the right way in the groups, doing what is required in this class. These things could possibly be said to be part of being a subject expert, but only in the cultural sense of having the right implicit skills: not in the sense that they are facts and ideas written in the textbook.
It is likely that they don't need much validation of this kind at all: but that they may need some. For instance Jim Baxter gave feedback to a class of 550 by selecting the best two bits of submitted groupwork each week and circulating them to the whole class along with comments on what made them the best. Students can do a remarkable amount of self-judgement but they do need some point of comparison.
This can be done in small classes by staff are circulating and listening in on groups, and occasionally commenting. This was probably done by Aronson and Ann Brown, judging by the descriptions, but this issue was not brought out. However it is an issue or constraint to bear in mind as class sizes rise; and also, has to be thought about in versions of Jigsaw mediated by software where the teacher isn't visibly circulating.
Another method, described by Ann Brown, is occasional benchmark lectures.
Issue 8: What size is best for groups?
Phase 1c: What is the best size for a group for productive discussion?Why does SLH design work?
Experts, and teachers, often have firm opinions on the best size for groups; but they do not agree with each other. There are a number of reasons for this, including that better individual skills makes for better group functioning (so optimal size can depend on learner's skills), larger groups take longer to settle down to optimum functioning, age etc. However the most important reason is that the best size for a group depends on what the group is doing. In deciding on your preferred size for each type of group, this is what to consider first.
Some constraints or issues (partly conflicting) on optimal group size.
- In Jigsaw designs, each cross-teach group must have one learner for each
different topic as a minimum. (And that could vary from week to week with how
the teacher thinks the overall topic can sensibly be divided.) If there is an
extra learner in the group, some topic will have not one but two "experts" on
it. This potentially diminishes the responsibility, and so pride after
success, of the learners. This is an argument for preferring the minimum size
for cross-teach groups (one person per topic).
- On the other hand, having two (or even more) people per topic in each
cross-teach group means that the presenter will be much less anxious because
their fellow expert can remedy any omissions they make. Thus larger self-teach
groups can be less stressful for cross-teaching. Furthermore, if groups remain
stable over multiple cycles (e.g. repeating once a week, with different
subjects) then they can take turns to take the lead in presenting, and to
support the other; and so each will have a turn at presenting. This is an
argument for larger cross-teach groups.
- In practice we must expect some absences on any given day, so having two
experts per topic in each group can also usually cover for that. Otherwise,
other members of that cross-teach group would never learn about that topic.
This is another argument for larger cross-teach groups.
- The self-teach / experts groups can be any size on the face of it. In
practice, it depends on what exactly they do in the groups. If they are all
well-prepared, then they might practise their presentations in turn, getting
others to critique them. Probably group sizes of 3 would be best, to maximise
the time each has to present, while still getting at least 2 sets of comments.
- If they are well-prepared in the sense of having read the material but are
not confident in their understanding, then discussing the meaning is the
central task. Good results are often had with pairs for this, though larger
numbers guards against getting stuck with others who have the same problem, or
the same (unfounded) agreement on the meaning. Here optimal outcomes will
depend less on having some optimum number in the group than on having a mix of
opinions in every group or pair.
- If they are very varied in how well prepared they are, then these
self-teach groups are remedial in nature, and in effect we will have a two
tier cross-teach design, where in the "self-teach" groups a well prepared
student teaches the unprepared (and gets better at this by practice in the
light of the questions they ask). In this case, they need to sort themselves
out into groups with at least one well prepared student in each.
Thus this solves the problem of large variations in effort (motivation) between students, where it exists (often in first year); but tends to require larger self-teach groups (six rather than three, say).
- In variants of Jigsaw where self-teach groups are authoring large materials
(rather than short oral presentations), then each such group is likely to
split itself up and each produce separate sections. In this case small group
sizes could be better, so that the joint product doesn't lose overall
coherence. It is natural for joint product groups to make a division of
labour, but to be less good at combining the parts. Furthermore, in all joint
product tasks, the bigger the group the more effort has to go into
inter-communication rather than into direct production.
- Another issue is validation of student (group) activity by staff
("Issue 7"). This may favour having larger groups so that staff can listen in
on them, occasionally commenting (and correcting or validating).
However as class sizes rise, this cannot be a sustainable approach, and some
other way of addressing validation will have to be used.
What size audience is best?
SLH, Jaye's classes.
Phase 2: Fragmenting self-teach groups (Issue 9)
With a doubling of class size, but retaining the number of topics as about 4 so that it is reasonable to accomplish the cross-teaching in one session, then the self-teach groups get too big to function as one. But splitting them up is perfectly sensible and easy. Various factors with a bearing on the best group size are discussed above under Issue 8 (ideal group size). For example:- Class size = 60.
- Distinct topics learned: 4
- Self-teach (expert) groups: 4 groups of size 15
↔ 12 groups of size 5, 3 groups for each topic.
↔ 20 groups of size 3, 5 groups for each topic. - Cross-teach (jigsaw) groups: 15 groups of size 4.
- In this case every learner prepares 1 topic, hears all 3 of the other topics, and gets to teach 3 other students about their own topic.
| If it is all taking place in one big hall, then it may be enough to tell learners to congregate in 4 areas for self-teach, as in the diagram which can be projected as a slide, then fission into 3 subgroups within each area. | 
|
Alternatively, you could calculate the split on the spreadsheet and allocate 12 self-teach groups, which would probably be best if they have to arrange their own time and place to meet.
This has already introduced the feature of duplicate authoring, where rival self-teach groups may produce materials or presentations addressing identical topics, but do so independently. This is implicit in all jigsaw self-teach groups, but will remain unreconciled (i.e. the best understanding and presentation ideas will not now be merged) as numbers grow and self-teach groupings fission.
Phase 3: Prioritising real, interactive cross-tutoring and learning by students (Issue 10)
As class numbers rise further there seem to be two main ways of developing Jigsaw designs: prioritising EITHER face to face cross-teaching OR original authoring. In this section we address the former.In this approach as class numbers rise, true face to face interactive cross-teaching is maintained, with all students exchanging their understanding in small groups (e.g. of 4). This could be the only way to get real interactive (discussion based) learning and teaching in mass classes: use Jigsaw.
Self-teach or expert groups become huge, and are subdivided as discussed above. A way of modifying the procedure so as to take advantage of the large numbers and get some cross-fertilisation between subgroups who are authoring the same topic might be to have not two main steps as in basic Jigsaw (time with the self-teach group, then time with the cross-teach group) but:
- Own (small) author i.e. self-teach group, creating a presentation or written materials in collaboration.
- Cross-critique other author groups doing the same topic: each from the original group split up and visit, say, four others; exchanging comments or perhaps giving a trial talk and getting feedback from this knowledgeable audience.
- Cross-teaching.
- Example table
- Class size = 83.
- Distinct topics learned: 6
- Self-teach (expert) groups: 6 groups of size 13-14
↔ 18 groups of size 4-5, 3 groups for each topic. - Cross-teach (jigsaw) groups: 14 groups of size 6-7.
- Class size = 83.
- Distinct topics learned: 4
- Self-teach (expert) groups: 4 groups of size 20-21
↔ 20 groups of size 4-5, 5 groups for each topic. - Cross-teach (jigsaw) groups: 20 groups of size 4-5.
- Class size = 181.
- Distinct topics learned: 3
- Self-teach (expert) groups: 3 groups of size 60-61
↔ 45 groups of size 4-5, 15 groups for each topic. - Cross-teach (jigsaw) groups: 60 groups of size 3-4.
- Class size = 660.
- Distinct topics learned: 3
- Self-teach (expert) groups: 3 groups of size 220
↔ 165 groups of size 4, 55 groups for each topic. - Cross-teach (jigsaw) groups: 220 groups of size 3.
- Class size = 5,000 e.g. MOOCs.
- Distinct topics learned: 3
- Self-teach (expert) groups: 3 groups of size 1666-1667
↔ 1221 groups of size 4-5, 407 groups for each topic. - Cross-teach (jigsaw) groups: 1666 groups of size 3-4.
You may think it better to have, in cross-teach groups, two rather than one expert for each topic as this reduces anxiety in the presenters. If the Jigsaw is repeated more than once (for different subjects) then each pair can alternate as to who leads. However this doesn't change the pattern as class size rises e.g.:
- Class size = 181.
- Distinct topics learned: 3
- Self-teach (expert) groups: 3 groups of size 60-61
↔ 45 groups of size 4-5, 15 groups for each topic. - Cross-teach (jigsaw) groups: 30 groups of size 6-7.
What is the value of direct cross-teaching?
By direct cross-teaching, I mean face to face in a small group, so that it is dialogic teaching, not a monologue which would be better written. Some of the arguments for dialogic teaching, and having learners practise doing it, are:- They should have practice giving talks, not only at writing.
- They should have practice at teaching in a dialogue: not just delivering a monologue from a stage. It is just as bad to miss this out from training, as it is to miss out giving talks; and the poor quality of some Graduate Teaching Assistants shows the consequences of doing so. If lectures should be avoided in favour of discussion (and having learners read the basic material in advance), then shouldn't this argument be applied equally to peer teaching in Jigsaw designs?
- Such dialogues tend to increase the "presenter's" understanding as well as the hearers'. Trying to teach something for the first time is one of the most learning-promoting activities any student can do.
One question is what the right size for such a cross-teach group is. The smaller the more likely it is that each learner is able to ask any questions they need to ask. On the other hand, it may be true that having more than one "expert" for each topic makes it flow better, by having them support each other. Having more than one expert per topic in each cross-teach group also makes the design much more robust against student absences. In that case, the minimum cross-teach group size will be twice (or thrice) the number of topics, rather than only once.
Phase 4: Prioritising original authoring: student generated content (Issue 11)
The other line of development is to prioritise original authoring, where each small learner group prepares something different from the rest of the class. This means the number of topics grows with the size of the class; and as a consequence, learners cannot learn all the other topics created by other students. This might be preferable if you judge that the pedagogic value of authoring is even greater than taking part in interactive learning; and this does fit with courses designed (as so many are) to examine only a fraction of the materials "covered" or offered or allowed.Another reason for this approach is that there are some kinds of material that do subdivide in this way into huge numbers of items that constitute a useful whole. E.g.
- Having students author test questions (MCQs). < ref>
- Vocabulary items for learning a foreign language. Easy to get them to create entries for words (or a dozen words per group) not in the core vocabulary of the textbook.
- Constructing a really big resource, using a large class. E.g. collaboratively to create a Dictionary of Psychology / Geology etc.: one entry per team. An encyclopedia of Positive Psychology.
- Combinatorial exercises.
Having students create exercises (for their own class) in cases where a
really thorough set of exercises would deal with all combinations of elements
(not just the one new element being taught, or all elements so far jumbled
together). For example in maths, you might want learners to be able to add,
subtract, multiply, divide, and calculate exponents (e.g. two cubed),
perhaps for complex numbers rather than integers; and to do this in any
combination. That is 5 elements. Each separate group task is defined by which
of these elements is and is not to be included. With 5 elements, there are
2^5 = 32 combinations, so 32 "topics" for groups. With 10 elements, there are
over a thousand distinct combinations (topics for groups). The group that
gets in,out,in,in,out has to create exercises using addition, multiplication
and division (but not subtraction or exponents). If, for instance, the
exercises involve both adding and multiplying then they will involve questions
of association i.e. does 'a + b * c' mean '(a+b) * c' or 'a + (b * c)'? So more
elements is likely to mean more complex issues, but examples with only a few
terms (2 or 3 terms like a,b,c in the example); while fewer elements allows
more terms (e.g. adding a thousand numbers, or bigger numbers). Pedagogically,
it is easier to learn one element at a time; but learning to combine them is
also important: but requires different exercises.
Similarly in an introductory course on computer programming: variable declarations, initialisations, while loops, subroutines, expressions etc. need soon to be exercised together, not separately. Even in History you could consider this, where the elements might be a set of theoretical perspectives (e.g. Marxist, Feminist, military technological determinism, social history) and a set of time periods (the 1830s, the 1940s). Exercises with a single theory would require a deeper analysis, while those with several will be "compare and contrast interpretations" exercises. Exercises are time-consuming for teachers to construct; but a big class can generate a large bank of them for learners to select from.
Issue 12: Indirect topic coverage
A way of modifying the procedure so as to take advantage of the large numbers and get some cross-fertilisation between subgroups who are authoring different topics might be to have not two main steps as in basic Jigsaw (time with the self-teach group, then time with the cross-teach group) but:- Own (small) author i.e. self-teach group, creating a presentation or written materials on collaboration.
- Cross-teaching.
- Report back in author groups: what is best out of the other topics each of you has heard about?
Given this procedure, then the number of topics each student may hear about is given by the formula for indirect topic coverage given in section "B2: The numbers" above. However as the examples below show, this only helps for a bit, and as class size grows even further it eventually becomes entirely ineffective.
Examples of this line of development
- Class size = 83.
- Distinct topics learned: 18
- Self-teach (author) groups: 18 groups of size 4-5.
- Cross-teach (jigsaw) groups: 14 groups of size 5-6.
- Coverage with report-back: ≈ 17 of 18 topics.
- Class size = 181.
- Distinct topics learned: 60
- Self-teach (author) groups: 60 groups of size 3-4.
- Cross-teach (jigsaw) groups: 36 groups of size 5-6.
- Coverage with report-back: ≈ 13 of 60 topics.
- Class size = 660.
- Distinct topics learned: 165
- Self-teach (author) groups: 165 groups of size 4.
- Cross-teach (jigsaw) groups: 132 groups of size 5.
- Coverage with report-back: ≈ 17 of 165 topics.
- Class size = 5,000 e.g. MOOCs.
- Distinct topics learned: 1666
- Self-teach (author) groups: 1666 groups of size 3-4.
- Cross-teach (jigsaw) groups: 1,000 groups of size 5.
- Coverage with report-back: 13 of 1666 topics.
Conclusion
It is thus clearly possible, even for huge class sizes, to have every learner in a class do both some original authoring, and some dialogic teaching in a small group. The only thing that cannot be maintained in this case is having all students learn all the topics created by other students: i.e. "coverage" becomes poor.Ths will affect the motivation for learners using each others' products. With a small number of topics, which all learners are taught, you can arrange that all learners really need to understand this material e.g. by testing it in exams without a choice of topic. When there is more material (topics) than a student can learn (or the Jigsaw can teach to all), which is quite common in university courses, then you have to consider the motivation for using it even more carefully than normally. On the other hand, if all the material on the whole course comes from one student or another, then this is not a particular problem.
The next design issue (12) in developing this line is whether or not to subdivide the class into subsets with good cross-cutting interaction (only) within each of these subsets; or whether to take care to inter-connect the whole class in one huge network.
Phase 5: Degenerate group sizes. Can it make sense to have either group of size 1?
No: not and remain a Jigsaw design as defined above; but Yes: it can make important pedagogic sense.They are no longer, by my definition, Jigsaw designs and yet they are useful pedagogic learning designs which I admire, and which bring out things that are valuable in groupwork and which help us understand Jigsaw more deeply.
Reciprocal Peer Critiquing
Crossteach group size = 5-20 (say); self-teach size = 1, topics = ?.
Patchwork text
Crossteach group size = 6 (say); self-teach size = 1, topics = 6.
Each student has a personal topic (e.g. their own essay title; or reflecting on their own past professional practice). By presenting to each other, they get personal feedback on a topic that is generally similar to each other, but completely different in the specifics, and in the personal significance.
These two cases involve students who are learning different things in terms of concrete cases, but the same things at an abstract level (e.g. how to write that kind of essay).
SLH tutorials
Class: 14; topics = 3; Self-teach: 3 groups of 4-5;
Cross-teach: = 1 group of 14.
But could have been:
Class: 14; topics = 3; Self-teach: 3 groups of 4-5;
Cross-teach: = 2 groups of 7.
Presentation practice
Self-teach size = 3; topics = 1; cross-teach size = 3. [concrete view]
Self-teach size = 3; topics = 1; cross-teach size = 0. [abstract view]
Here the exercise is for each group member to prepare the same topic, and in turn present to the others; for critiquing on presentation technique. They steal methods from each other; and practise critiquing as well as generation (authoring). It relies on the knowledge being already in their heads (more or less), and improves method. This is also a good revision technique, in contrast to a common technique of dividing the knowledge work amongst a group (as in a conventional Jigsaw).
My year 4 courses
Self-teach size = 6; topics = 18; cross-teach size = plenary.
Problem is: making students really use each others' products.
Collected summaries of group allocations in Jigsaw designs
This table collects together summaries of all the cases of Jigsaw design mentioned.
| Sorted by class size | Sorted by number of topics | |
| |
|
B4: Rough list of design decisions
Group allocation design decisions
If you are designing a Jigsaw activity, and making allocation decisions, then here is a rough list of the design decisions you must take.- (Given the class size is fixed, known.)
- Decide whether the Jigsaw process is done once in that course / semester, or is repeated weekly or daily.
- If repeated, then will you maintain group membership throughout the
course, or "remix" groups each time?
- The number of topics (that the overall subject is to be divided into) e.g. 3 or 4.
- Preferred number to have in cross-teach groups (i.e. the preferred number of experts / topic in each cross-teach group e.g. 1 or 2).
- How to achieve usage by learners of their peers' products. I.e. why would students need to learn in the cross-teach groups? (See below for more.)
- If the class is large, decide which to give priority to: personal teaching, or original authoring by each learner.
- Build in report-back step? yes/no
- Build in expert cross-critiquing step within expert pools? yes/no
- Student knowledge delivered by a) exposition, or b) exposition with
dialogue; or c) reading / JustInTime style interactive session which assumes
reading.
- Self-teach: minimum, maximum size of groups, number of groups (decide one of these three numbers and the others are more or less decided too).
- Cross-teach: minimum, maximum size of groups, number of groups (decide one of these three numbers and the others are more or less decided too).
Wider course design issues
Good choices for these may solve some of the issues above; and certainly are likely to affect the pedagogic success of the whole activity.- Is the subject for the whole Jigsaw suitable? One that will benefit from discussion?
- Are the subtopics suitable? both self-contained enough to study, but inter-dependent enough to make the cross-teaching matter.
- Consider giving the students a voice in creating and/or selecting the subtopics.
- Why would students need to learn in the cross-teach groups?
Three general alternative answers to this:
- An exam covering all the topics. (This might become visible as notes taken for future revision.)
- Because you have arranged for Cross-Teach groups to themselves give a talk / write materials for an outside audience on how the topics combine into an overall idea.
- Some other project they are required to do where they have to combine the topics.
- What concrete deliverables will you formally require from each student
(other than group participation)? E.g.
- Written material (web or paper) from the self-teach groups?
- Oral presentations from the self-teach groups to the class or to a cross-teach group?
- Written material (web or paper) from the cross-teach groups?
Part C: problems, design issues
(if , when) Students don't like Jigsaw
Late comers to the class / dropouts
See my comments in the section "Issue 6".Learning on the spot
In a school classroom, the idea is usually accomplish the learning in one period: say first half of the time might be self-teach groups prepare to present; second half of the time, move back to their jigsaw groups and teach each other. In these cases the number of topics is probably going to be about 3: that then, is the min. and ideal size of the jigsaw groups; and equally it is the number OF self-teach groups (one per topic). For instance:- Class size = 25.
- 3 groups of 8 or 9 for expert/ self-teach groups.
- 8 groups of 3 or 4 for jigsaw / cross-teach groups.
In practice, although there will only be 3 kinds of self-teach group, one per topic, it may be better to subdivide these into groups of 3 or 4 (no exact plan is necessary).
Thus in a CPD presentation about Jigsaw, you can use this kind of plan for a demo so that the audience can experience it. Again 3 (say) topics (perhaps presented on briefing sheets). Any number in the "class" i.e. audience. Organise / impose jigsaw groups of 3 each, 4 to take care of odd numbers. For instance:
- Audience size = 100.
- 3 groups of 33 or 34 for expert/ self-teach groups; naturally will fragment into smaller subgroups e.g. of 3 or 4.
- 33 groups of 3 (or 4) for jigsaw / cross-teach groups.
With some advance homework
In many cases, both school and first year university, you may get the students to do some or all of the self-teaching in advance; any meeting of the self-teach groups is then used for those who did little homework to catch up from those who did more; and use scheduled class time mainly for the cross teaching.
Putting off the main learning
In final year undergraduate courses, you may shift it further so that the main student work is preparing materials for other students e.g. to use at revision time. This fits with the usual unofficial course design in which term time is a minor part of the story, and the real learning goes on during revision.Redefining "cross-teaching"
Alternatively, redefine cross-teaching as:- All must pre-read the material prepared by others in their jigsaw group
- Meet face to face and discuss: contribute both critiques, clarification questions, and discussion of the concepts and meanings.
Spreading or repeating over time
The original Jigsaw was a pattern (learning design) for one class period, which was then repeated perhaps every class meeting.Next (sketched above), there is some homework plus a central class meeting. This can then be repeated, cycling over topics and over people. For instance Honeychurch (2012) had a different topic each week; and a different member of the expert groups (which stayed the same for the semester) had to make the presentation to the class, thus ensuring each had a turn (like it or not).
Another pattern was used by me (Draper, 1998) where each group had to produce a public web page with notes for one week's lectures. Thus they had to do the work in one week (pre-scheduled), but benefitted from the work the rest of the class did in the other weeks.
Problems / symptoms
- Members of a self-teach group subdivide the work and don't produce a true joint product.
- No cross-teach event happens: only material for later solo learning.
- Learning is only done during revision time.
- Use class time for cross presentations
- Perhaps JITT (just in time teaching): require the class to pre-read the material, answer questions online both to enforce this and to give the presenter indications of what to spend face to face time on.
- Go for a big room: each author group splits up (could have 6 of these in a room).
- But I would have to assign and enforce these meetings; allocate contact time, ...
Other links
Here is a spreadsheet with the formulae I use for generating jigsaw groups for a class. Whether it is usable by others, I'm not sure. hereReferences
The main references on Jigsaw are given in the parent page and section.
Baxter, J. (2007) "A Case Study of Online Collaborative Work in a Large
First Year Psychology Class" The REAP International Online Conference on
Assessment Design for Learner Responsibility, 29th-31st May, 2007
Available at:
local copy
(2,
3).
Available
from this site
here.
[A description of a learning design using peer interaction, not tutor
marking for feedback]
Brown, A.L., & Campione, J.C. (1996) "Psychological theory and the design of innovative learning environments: On procedures, principles, and systems" In L.Schauble & R.Glaser (Eds.) Innovations in learning: New environments for education (ch.11 pp.289-325) (Mahwah, NJ: Erlbaum)
Draper (1998) Computer Supported Cooperative Lecture Notes
Honeychurch,S.L. (2012) Taking Forward the Jigsaw Classroom: the Development and Implementation of a Method of Collaborative Learning for First Year Philosophy Tutorials (HEA) PDF
Scoggins,J. & Winter,R. (1999) "The Patchwork Text: a coursework format for education as critical understanding" Teaching in HE vol.4 no.4 pp.485-499 doi:10.1080/1356251990040405 [Patchwork Text]
Sherif,M. & Sherif,C.W. (1969) Social Psychology
(rev. ed.; New York: Harper & Brothers).
Quick summary
[Group bonding FROM joint action.]
Web site logical path:
[www.psy.gla.ac.uk]
[~steve]
[localed]
[jigsaw]
[this page]
[Top of this page]